Are you scouring the internet for 'write a conjecture about congruent chords in a circle'? You can find all the information here.
Table of contents
- Write a conjecture about congruent chords in a circle in 2021
- Congruent central angles
- Chord theorems
- Congruent chords are equidistant from the center of a circle
- Inscribed angle conjecture
- If a radius of a circle is perpendicular to a chord, then it bisects the chord
- The perpendicular bisector of a chord passes through the center of the circle.
- Two chords are congruent if and only if
Write a conjecture about congruent chords in a circle in 2021
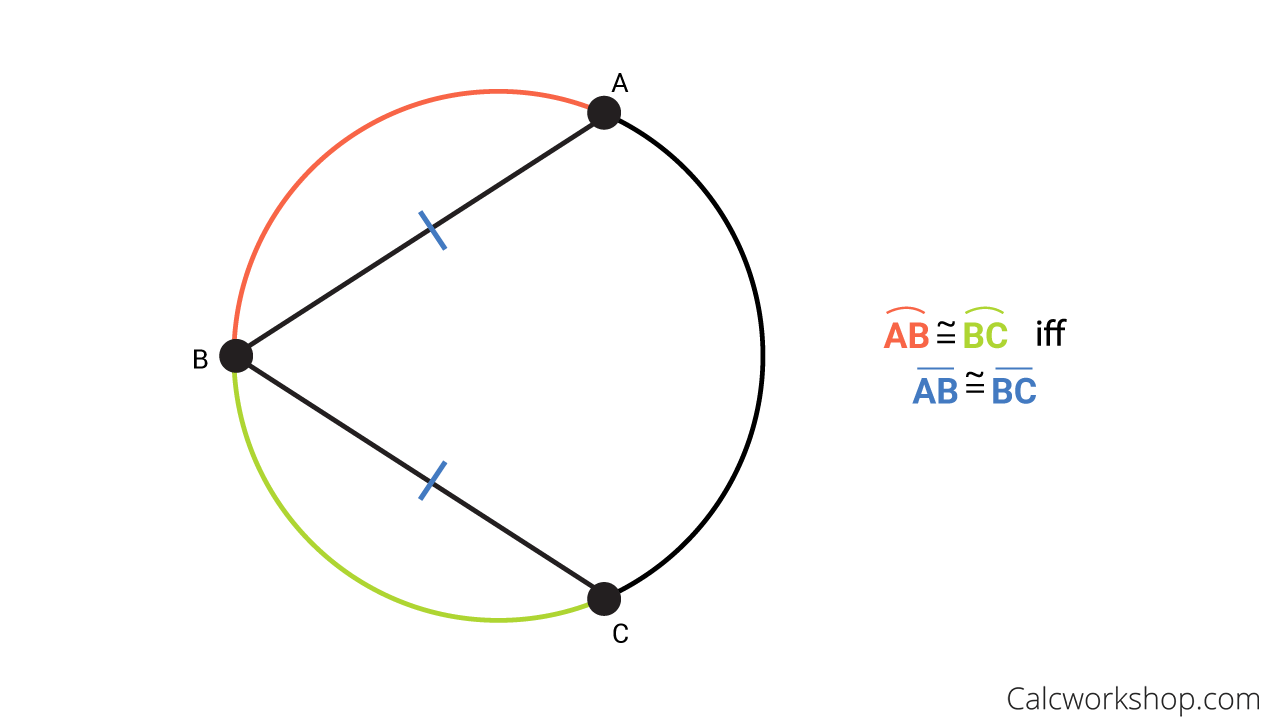 This picture representes write a conjecture about congruent chords in a circle.
This picture representes write a conjecture about congruent chords in a circle.
Congruent central angles
 This image representes Congruent central angles.
This image representes Congruent central angles.
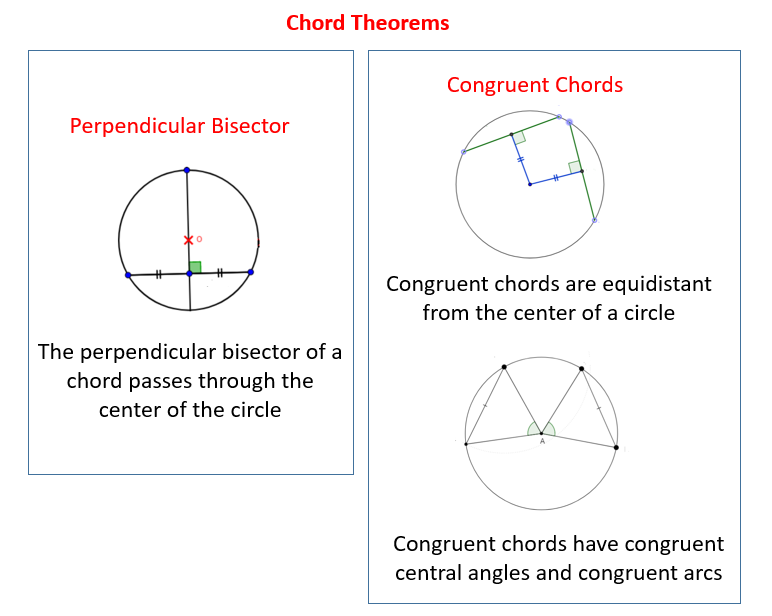
Chord theorems
 This image representes Chord theorems.
This image representes Chord theorems.
Congruent chords are equidistant from the center of a circle
 This image illustrates Congruent chords are equidistant from the center of a circle.
This image illustrates Congruent chords are equidistant from the center of a circle.
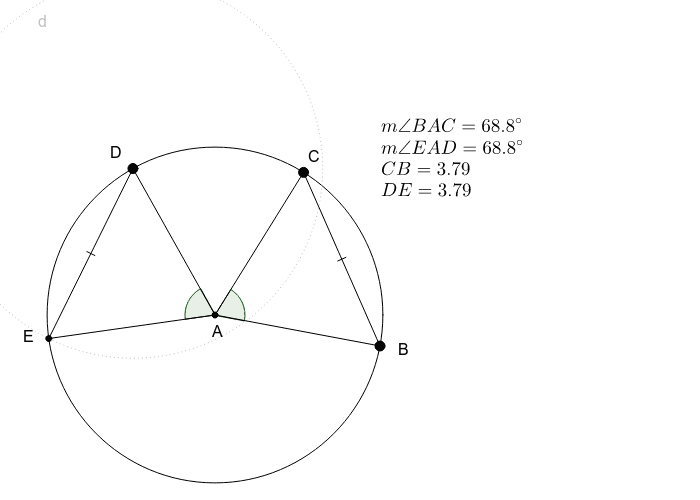
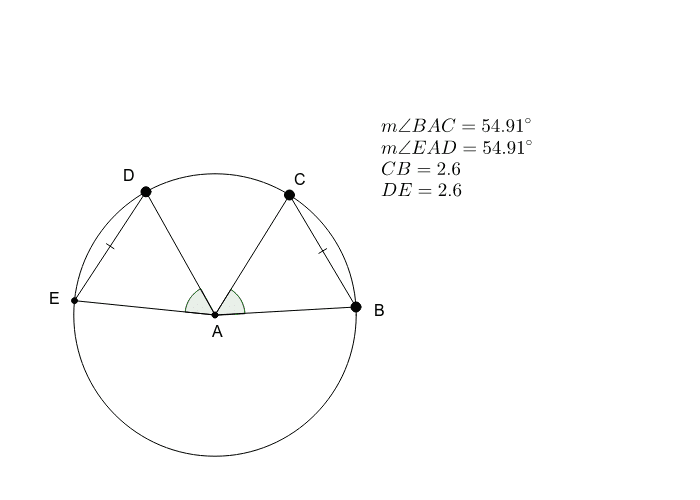
Inscribed angle conjecture
 This image demonstrates Inscribed angle conjecture.
This image demonstrates Inscribed angle conjecture.
If a radius of a circle is perpendicular to a chord, then it bisects the chord
 This image representes If a radius of a circle is perpendicular to a chord, then it bisects the chord.
This image representes If a radius of a circle is perpendicular to a chord, then it bisects the chord.
The perpendicular bisector of a chord passes through the center of the circle.
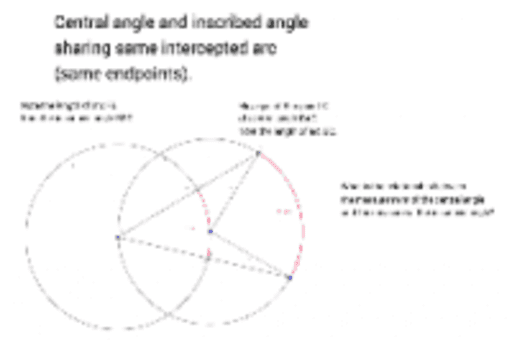 This picture illustrates The perpendicular bisector of a chord passes through the center of the circle..
This picture illustrates The perpendicular bisector of a chord passes through the center of the circle..
Two chords are congruent if and only if
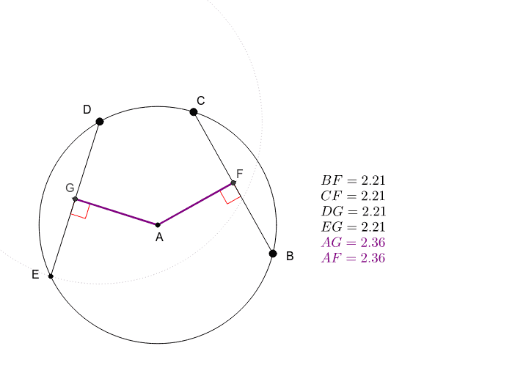 This picture shows Two chords are congruent if and only if.
This picture shows Two chords are congruent if and only if.
Which is the correct statement of the conjecture of congruent chords?
The precise statement of the conjecture is: Conjecture (Congruent Chords): If two chords of a circle are congruent, then they determine central angles which are equal in measure. If two chords of a circle are congruent, then their intercepted arcs are congruent. Two congruent chords in a circle are equal in distance from the center.
Is the distance from the center to two congruent chords equal?
This conjecture tells us that the central anglesdetermined by the congruent chords are equal in measure, which implies that the intercepted arcsare congruent. This conjectures also tells us that the distances from the center of the circle to two congruent chords are equal.
Are there chords in a circle that are congruent?
Congruent chords are equidistant from the center of a circle. Theorem: If two chords in a circle are congruent then their intercepted arcs are congruent. Converse: If two arcs are congruent then their corresponding chords are congruent.
How do you know if an arc is congruent?
Conjecture (Congruent Chords): If two chords of a circle are congruent, then they determine central angles which are equal in measure. If two chords of a circle are congruent, then their intercepted arcs are congruent. Two congruent chords in a circle are equal in distance from the center.
Last Update: Oct 2021
Leave a reply
Comments
Latunja
27.10.2021 11:00We can use the good old mathematician theorem. If a diam of a dress circle is perpendicular to a chord, past the diameter bisects the chord and its arc.
Tremone
27.10.2021 03:58Present are some additive geometric objects related to with circles. Then economic consumption your conjecture to find the adjacent item in the sequence.
Dauna
27.10.2021 02:11If and only if ab# bc theorem 10. Check out this tutorial to find out about circles!